Geometric Sequences and Series | ||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||
Introduction | ||||||||||||||||||||||||||||
This page will teach you about geometric sequences and series. These are the sections within this page:
MATHguide has a video with guided notes to help you understand geometric sequences. Access the guided notes and then proceed with the video. This activity/video addresses two Common Core State Standards: HSF.BF.A.1.A and HSF.BF.A.2.
If you rather, you can continue on with this text-based lesson to learn about geometric sequences and series.
| ||||||||||||||||||||||||||||
|
Sequences of numbers that follow a pattern of multiplying a fixed number from one term to the next are called geometric sequences. The following sequences are geometric sequences: Sequence A: 1 , 2 , 4 , 8 , 16 , ... For sequence A, if we multiply by 2 to the first number we will get the second number. This works for any pair of consecutive numbers. The second number times 2 is the third number: 2 × 2 = 4, and so on.
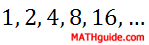
For sequence B, if we multiply by 6 to the first number we will get the second number. This also works for any pair of consecutive numbers. The third number times 6 is the fourth number: 0.36 × 6 = 2.16, which will work throughout the entire sequence. Sequence C is a little different because it seems that we are dividing; yet to stay consistent with the theme of geometric sequences, we must think in terms of multiplication. We need to multiply by -1/2 to the first number to get the second number. This too works for any pair of consecutive numbers. The fourth number times -1/2 is the fifth number: -2 × -1/2 = 1. Because these sequences behave according to this simple rule of multiplying a constant number to one term to get to another, they are called geometric sequences. So that we can examine these sequences to greater depth, we must know that the fixed numbers that bind each sequence together are called common ratios. Mathematicians use the letter r when referring to these types of sequences. Mathematicians also refer to generic sequences using the letter a along with subscripts that correspond to the term numbers as follows:
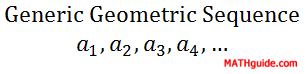
This means that if we refer to the tenth term of a certain sequence, we will label it a10. a14 is the 14th term. This notation is necessary for calculating nth terms, or an, of sequences. The r-value, or common ratio, can be calculated by dividing any two consecutive terms in a geometric sequence. The formula for calculating r is...
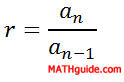
...where n is any positive integer greater than 1.
| ||||||||||||||||||||||||||||
To determine any number within a geometric sequence, there are two formulas that can be utilized. Here is the recursive rule.
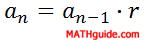
The recursive rule means to find any number in the sequence, we must multiply the common ratio to the previous number in this list of numbers. Let us say we were given this geometric sequence.
We can see that the common ratio is 3 because we have to keep multiplying by 3 to go from one term to the next. If we wanted to find the 5th term, we would multiply the 4th term by 3 to get 81. If we multiply the 5th term by 3 we get the 6th term, which is 243, and so on. What if we wanted to find the 20th number? We would have to find all off the numbers before the 20th number, if we use the recursive rule. That would be too much work. Instead, we will use this explicit rule.
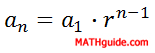
To find the 20th number, all we have to do is multiply the first number in the sequence by the common ratio raised to the 19th power, like this. a20 = (1)(3)20-1 a20 = (3)19 a20 = 11622615 | ||||||||||||||||||||||||||||
In this section, we will look at coming up with a unique formula to define all the terms in a geometric sequence. We will use the explicit rule to help us.
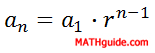
We will look at two examples to explain this skill. Example 1: Calculate the formula for sequence A, seen below, and use it to find the 9th term in the sequence.
The fixed number, called the r-value or common ratio, is 2. The first term, a1, is 1. Now we use the explicit rule to gain a formula, like so. an = (1)(2)n-1 an = 2n-1 a9 = 29-1 a9 = 28 a9 = 256 Example 2: Find the formula for sequence B, seen below, and use it to determine the 15th term in the sequence.
The common ratio or r-value is 6 because we have to keep multiplying by 6 to go from one term to the next term. The first term, a1, is 0.01. We will now see how the explicit rule helps us to find the formula. an = (0.01)(6)n-1 a15 = (0.01)(6)15-1 a15 = (0.01)(6)14 a15 = 78364164
| ||||||||||||||||||||||||||||
Let us look at an example where we are given a sequence of numbers and we have to find how many numbers there are in the sequences. Example: Find the number of terms in the sequence 1, 2, 4, 8, 16, ..., 256. First, we will develop a formula for this sequence using the explicit rule. The first term, a1, is 1 and the common ratio is 2. an = (1)(2)n-1 an = 2n-1 256 = 2n-1 log(256) = log(2n-1) log(256) = (n - 1)log(2) log(256)/log(2) = (n - 1) log(256)/log(2) + 1 = n 9 = n n = 9 | ||||||||||||||||||||||||||||
Given our generic geometric sequence...
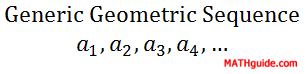
...we can look at it as a series.
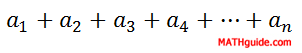
As we can see, the only difference between a sequence and a series is that a sequence is a list of numbers and a series is a sum of numbers. There exists a formula that can add a finite list of numbers and a formula for an infinite list of numbers. Here are the formulas... 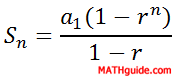 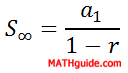
Example 1: Find the sum of the first 7 terms of the sequence below.
The sum formula requires us to know the first term [a1], the common ratio [r], and the number of terms [n]. We know the first term is 1. The common ratio is 2. The number of terms is 7. Plugging this information into the formula give us this. 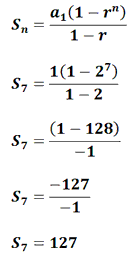
Example 2: Add the first 10 terms of the sequence below.
We can see a1 = 0.01, r = 6 and we were told n = 10. We would then plug those numbers into the formula and get this. 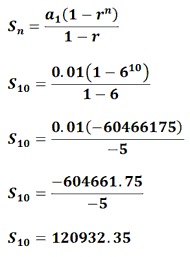
Example 3: Add the infinite series 16 + (-8) + 4 + (-2) + 1 + ... The only way we can add an infinite series is for two conditions to be met: a) it has to be a geometric series and b) the common ratio has to be greater than -1 but less than 1. Looking at the series, we can see that there is a common ratio. This means it is geometric. Since the common ratio is -1/2 and it falls between -1 and 1, we can use the sum formula. We will use a1 = 16 and r = -1/2. 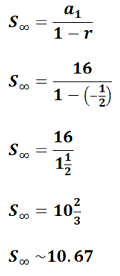
Example 4: Add the infinite sum 27 + 18 + 12 + 8 + ... We need to check the conditions to see if we can use the infinite sum formula. It does have a common ratio. It is 2/3. Since 2/3 is less than 1 and greater than -1, we can use the formula, like this. 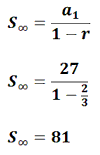
|
Here are the available videos for this content:
|
After reading the lesson, try our quizmaster. MATHguide has developed numerous testing and checking programs to solidify skills demonstrated in this lesson. The following quizmasters are available:
|
After reading the lesson, try a related lesson.
|
 ideo:
ideo:  ctivity:
ctivity:  uizmaster:
uizmaster:  esson:
esson: