Sigma Notation: Arithmetic Series | ||
| ||
Introduction | ||
In this lesson, you will learn how to work with sigma notation. Here are the sections in this lesson. Before studying sigma notation, it is required that you first have a firm grasp of these mathematical topics.
|
We will review sigma notation using another arithmetic series.
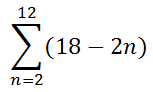
To find the first term of the series, we need to plug in 2 for the n-value. To find the next term of the series, we plug in 3 for the n-value, and so on. We keep using higher n-values (integers only) until we get to our final value. Our final value is 12. This table will show us what those n-values are and their respective values evaluated within the expression.
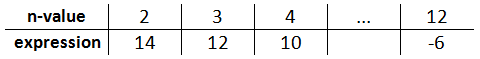
Now, this means we know the terms of the series.
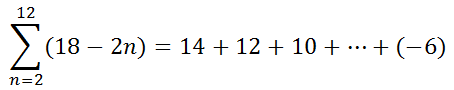
We can calculate the sum of this series, again by using the formula. Be careful when determining the number of terms in this series. The number of terms is equal to one more than the difference between the final value and the initial value.
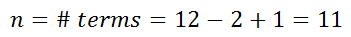
So, n = 11, a1 = 14, and a11 = -6.
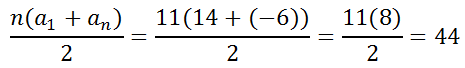
So, our solution can be written...
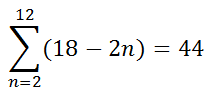
To ensure that you understand this lesson, try this interactive quiz. | |
Try this quiz, which is related to the sections above. | |
Try these lessons, which are related to the sections above.
| |
 esson:
esson:  uiz:
uiz: