Sigma Notation: Geometric Series | ||
| ||
Introduction | ||
In this lesson, you will learn how to work with sigma notation. Here are the sections in this lesson. Before studying sigma notation, it is required that you first have a firm grasp of these mathematical topics.
|
Here is a series written in sigma notation.
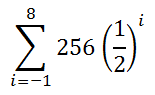
First, notice how that the variable involves an 'i'. Any variable can be used when dealing with sigma notation. So, an 'i' is no more significant than using an 'n'. Let us evaluate the expression for i = -1 to gain our first term. We get...
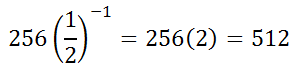
Evaluating the expression for i = 0 to gain our second term gives us...
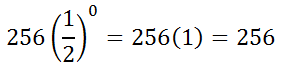
Evaluating the expression for i = 1 to gain our third term gives us...
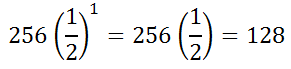
Evaluating the expression for i = 8 to gain our last term gives us...
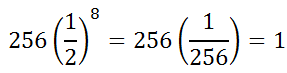
So, our sigma notation yields this geometric series.
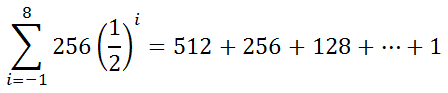
We can find this sum, but the formula is much different than that of arithmetic series. The formula is this.
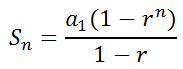
We will plug in the values into the formula. Keep in mind that the common ratio -- the r-value -- is equal to a half and the number of terms is 8 - (-1) + 1, which is 10.
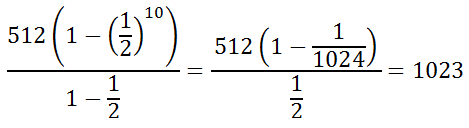
To ensure that you understand this lesson, try this interactive quiz. | |
Try this quiz, which is related to the sections above. | |
Try these lessons, which are related to the sections above.
| |
 esson:
esson:  uiz:
uiz: