Double Angle Formulas for Sine, Cosine, & Tangent | ||
| ||
Introduction | ||
In this section of MATHguide, you will learn about double angle formulas for sine, cosine, and tangent. Here are the topics within this page:
Before carrying on with this lesson, you must have knowledge of the sum angle formulas. If necessary, review these lessons before moving on with the next sections.
|
Here are the double formulas.
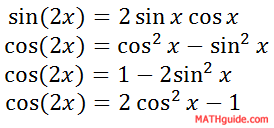
The next sections of this lesson will derive the double angle formulas using the sum angle formulas.
| |
We will start by looking at a Sum and Difference Angle Formula for Sine.
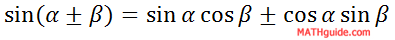
We can use the formula to find a sum, but we will make both angles the same angle.
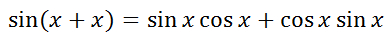
We can change the last term by multiplying in a different order.
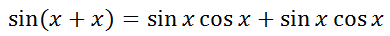
Using algebra, we can combine the terms of the right side of the equation. We can also add the angles together on the left side of the equation.
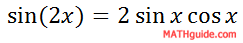
This is the double angle formula for sine.
| |
Like the previous section began, we will begin this section with the Sum and Difference Angle Formula for Cosine.
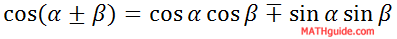
Take the case that there is a sum of two angles and the angles are the same.
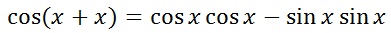
We can add the angles together within the left side of the equation and we can clean up the right side of the equation.
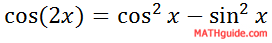
This is the first double angle formula for cosine. To get another formula, we first need to reflect on a Pythagorean Identity.
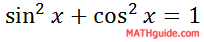
We can manipulate it by subtracting sin2x from both sides to get...
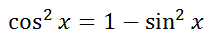
If we take this expression for cos2x and replace it within our first double angle formula for cosine, this is the result.
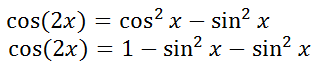
Cleaning up the expression by adding like terms takes us to our second double angle formula for cosine.
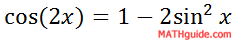
Going back to our Pythagorean Identity, we can subtract sin2x from both sides.
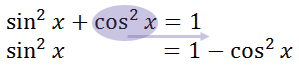
We can take this expression for sin2x and substitute it within the first double angle formula for cosine. This is the result.
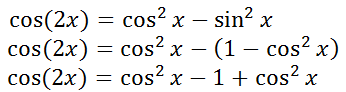
Adding like terms, we get our third double angle formula for cosine.
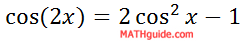
| |
Like our previous sections, we need to start with the Sum and Difference Angle Formula for Tangent.
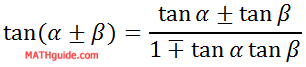
We can use the sum formula with two angles that are the same, like so.
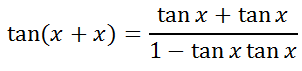
Cleaning up the formula leads to our double angle formula for tangent.
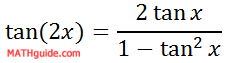
| |
It is natural to wonder, "Why are these formulas important?" The answer relates to problems that occur where an equation contains terms of different angles. Take this example.
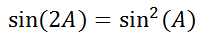
We can see that the left side of the equation has twice the angle A but the right side has simply the angle A. To solve this problem, the angles first have to match. Either both sides need to have twice the angle or the angle, but not both. Double angle formulas help us change these angles to unify the angles within the trigonometric functions. It allows us to solve trigonometric equations and verify trigonometric identities.
However, using these techniques will be reserved to a different section of MATHguide.
| |
Here are lessons that are related to the content above.
| |
 esson:
esson: