Exponential Functions | ||
| ||
Introduction | ||
This lesson will inform you of the properties of exponential functions. Here are the sections within this lesson page:
|
Exponential functions are functions that are in this form.
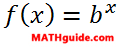
We refer to the b-value as the base and the x-value as the exponent.
| |
If the base of the function is greater than one (b > 1), then we say the function is a growth function. If the base of the function is greater than zero but less than one (0 < b < 1), then we say the function is decaying. The distinction is not trivial. The graphs of growth and decay functions look different. Here is a comparison between the graphs of growth and decay functions.
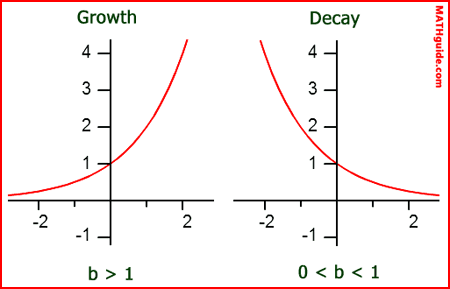
It can be clearly seen that the graphs of growth functions rapidly go up to the right. Conversely, decay functions drop quickly and then level out to the right.
| |
The y-intercept is an important location within the graphs of exponential functions. To mathematically find them, simply substitute zero for the x-value within the function. We substitute zero for 'x' because all points on the y-axis have an x-value equal to zero. For instance, if we needed to locate the y-intercept of the function...
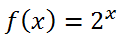
...we would substitute zero for the x-value. Since any number to the zero power is equal to one, we know the y-intercept is (0,1). (See our Power Rules lesson for a refresher on this property.) This is confirmed if we examine the graph of the function (see below).
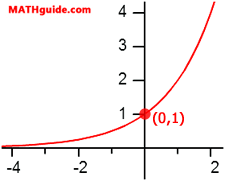
If we examine the general case, we will find the same result. Look at the general form of an exponential function.
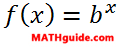
If we substitute zero for the x-value, we will find that any number raised to the zero power (except zero) is equal to one. Which means exponential functions of this form always have a y-intercept of (0,1).
Keep in mind, however, that transformations of exponential functions will move the y-intercept.
| |
Exponential functions have asymptotes. An asymptote is a line (or a curve) that guides the graph of a relation. In the case of an untransformed exponential equation, the asymptote is on the x-axis. Take a look at the graph of the function y = 2x.
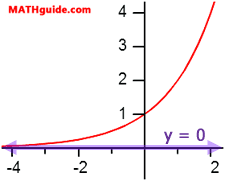
As we move on the curve from the right to the left (as x → - ∞), we see that the curve gets closer and closer to the x-axis (f(x) → 0). That is why the x-axis is acting like a guide for the exponential function. This is why the line y = 0 has been highlighted in purple over the x-axis -- so that it can easily be seen.
Again, transformations of exponential functions can move the asymptote.
| |
Try theses lessons, which are related to the sections above.
| |
 esson:
esson: