This lesson will inform you how to transform exponential functions. Here are the sections within this lesson page:

• Rules of Transformations
• Horizontal Shifts and the Y-intercept
• Vertical Shifts and the Asymptote
• Reflection Over X-Axis
• Transformation: Examples
• Instructional Videos
• Interactive Quizzes
• Related Lessons

    Transformations -- regardless of the function -- behave the same. This graphic organizer describes transformations on the function f(x).

    The sections below will describe how specifically an exponential function behaves under these transformations.

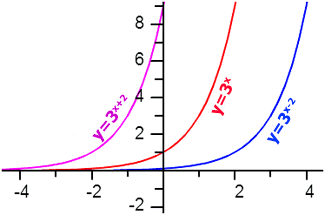
    If the x-variable of a parent function, f(x), is replaced with 'x + 2,' every point of the function will move 2 units left. Conversely, if the x-variable of a parent function, f(x), is replaced with 'x - 2,' every point of the function will move 2 units right.

    The graph below demonstrates this for the function...

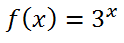
    There are two important points to notice.

1. Point 1: The asymptotes for the three functions are all the same. All of the asymptotes are y = 0 because horizontal shifts do not move horizontal lines. The asymptotes for exponential functions are always horizontal lines.

2. Point 2: The y-intercepts are different for the curves. Finding the location of a y-intercept for an exponential function requires a little work (shown below).

    To determine the y-intercept of an exponential function, simply substitute zero for the x-value in the function. The reason this works is because all points on the y-axis have an x-value equal to zero.

    Here is the mathematics for all three of the functions that have been graphed above. Colors have been added to match the graph in this section.

    These y-intercepts can be verified by examining the graphs in this section.

    uiz: Exponential Functions: Transformations

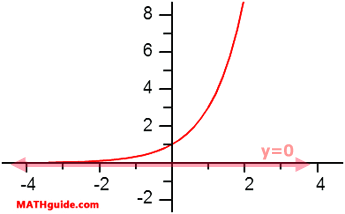
    The parent curve of an exponential function has the asymptote y = 0. This is evident by looking at the function...

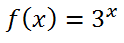
...which has been graphed below.

    Look what happens when we either add or subtract a number to/from our parent function.

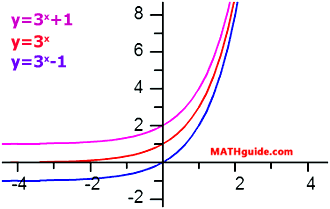
    Notice if we add the number 1 to the function that the function moves vertically up 1 unit. If we subtract 1 to the function, the function moves vertically down 1 unit. In both cases the asymptote follows the curve. The table below shows this close correlation.

    uiz: Exponential Functions: Transformations

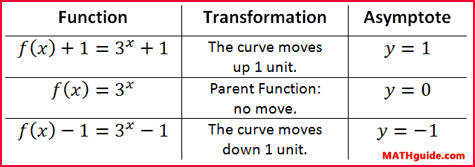
    If a function and its opposite are compared, we would see that they would be mirror versions of each other. The mirror would be the x-axis, in this situation.

    We should look at a specific situation. Let us examine our parent function from a previous section and its opposite function.

    Here are their graphs.

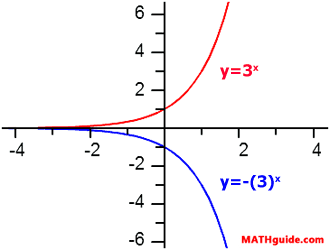
    This demonstrates how the transformed function is obtained by flipping the original function over the x-axis.

    Now that we have seen several types of transformations, we will now look at a few examples.

Example 1: g(x) = 4^x+2 + 1

    Let's first determine how this function compares with its parent function, which is...

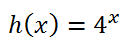
    To graph g(x), we would have to move h(x) 2 units left and 1 unit up.

    The number next to the x-value is the horizontal shift and we have to take the opposite to determine the direction of the shift. The +2 really means 2 units left. The +1 is not next to the x-value, which means it is the vertical shift number.

    Now, we can sketch the graph of g(x) since we have a general idea of the shape of h(x), which is an exponential growth function.

    The asymptote of h(x), which is y = 0, will shift up 1 unit along with g(x). This will make the asymptote of g(x) equal to y = 1.

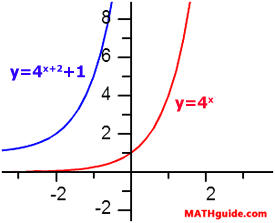
    To locate its y-intercept, we need to substitute the value 0 for the x-value, like so.

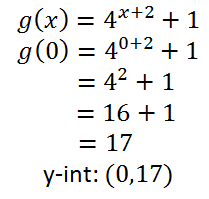
Example 2: k(x) = -2^x-1 - 3

    This transformation requires reflecting k(x) over the x-axis, moving the curve 1 unit right and 3 units down.

    The asymptote must be y = -3, since the curve was moved down 3 units.

    The y-intercept can be found as follows.

    uiz: Exponential Functions: Transformations

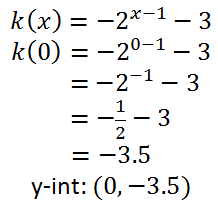
    This video will help you understand the transformation sections above.

    ideo: Basic Translations (Transformations) of Functions

    This quiz will help you master the lessons above.

    uiz: Exponential Functions: Transformations
    uiz: Exponential Functions: Practical Transformations

    Try these lessons, which are related to the sections above.

    esson: Translations
    esson: Translating Polynomials: Parabolas
    esson: Exponential Functions
    esson: Calculating Value Over Time
    esson: Geometric Sequences and Series
    esson: Logarithms