Limits of Piecewise Functions | ||
| ||
Introduction | ||
This lesson page will inform you how to find various limits of piecewise functions. Here are the sections within this page:
Likewise, an essential part of understanding the limits of piecewise functions is to first understand piecewise functions. Review this lesson to learn more about piecewise functions.
|
When we determine a limit of a function, we attempt to see if there is a trend. Without actually evaluating the function at a specific x-value, we look to see what is happening to the y-values as we get closer to a certain x-value. If we were given the function f(x) that has been graphed below, we can determine the limit of the function as we approaches the x-value -1. If we are left of the x-value -1 and we move to the right, the y-values get larger. As we approach the x-value -1, the y-values get closer to 1. View the graph to confirm this fact.
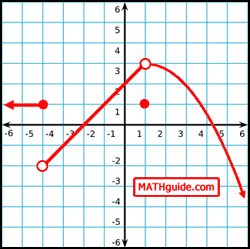
Likewise, if we are right of the x-value -1 and we move to the left, we will notice how the y-values get smaller. As we approach the x-value -1, the y-values get closer to 1. No matter if we approach the x-value -1 from the left or the right, the y-value approaches 1.
| |
Within the last section (see Evaluating Limits), we performed two limits. The first limit can be written like so.
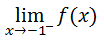
It is pronounced as 'the limit of f(x) as x approaches -1 from the left. [The negative sign that is hovering on the -1 that looks like it is in the exponent position is the clue that we are being asked to approach the x-value -1 from the left side of -1.] Similarly, we can write the limit as we approach the x-value -1 from the right side, like so.
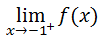
Again, the plus sign that is hovering in the exponent position mean that we are being asked to approach the x-value -1 but this time from the right side of -1.
| |
There are two cases that can happen when dealing with limits. Case 1: The Limit Exists For some a-value, if...
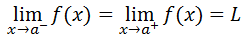
...then...
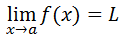
Case 2: The Limit Does Not Exist For some a-value, if...
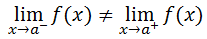
...then...
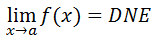
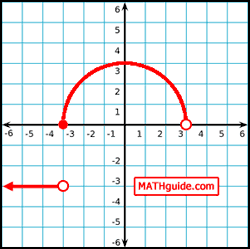
DNE is shorthand for 'does not exist.' We already saw an example of case 1 (see the example within Limit Notation). So, we will examine a situation for case 2. The graph below is of g(x). We will use this graph of g(x) to determine the following limit.
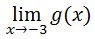
To determine this limit, we have to first consider both of these limits separately.

First, we will consider this limit.
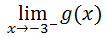
To calculate this limit, we have to approach the x-value -3 from the left side. We have to observe the y-values and see where they are headed as we move to the right, closer to the x-value -3. As we move closer and closer to the x-value -3, we can see that the y-values remain constant at -3. Now let's calculate the other limit.
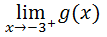
We are being asked to approach the x-value -3, but from the right side of -3. As we move left along the curve, we eventually slide downward on the left side of the semi-circle. As we get closer to the x-value -3, we can see the y-value is moving toward 0. Notice how the two limits are not equal.

Since the two limits are not equal, we say...
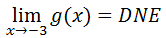
...which means the limit 'does not exist.'
| |
This instructional video will demonstrate how to evaluate limits. | |
Try this interactive quiz, which are related to the sections above. | |
Try these lessons, which are related to the sections above.
| |
 esson:
esson:  ideo:
ideo:  uiz:
uiz: